
This tutorial is an advanced version of creating grass using displacementMod. Instead of displacing the grass with a heightmap, we’re going to use the Fur modifier to generates the grass as geometry at render time.
The cool thing about it is that you have quite a lot of control over the size, bend amount, direction variation, randomization, density, and more. Plus, you can even use custom maps to shape and manipulate all of these parameters.
Below the video, you can see an explanation of how an RGB image can affect the bend direction of the grass shown at the end of the tutorial.
Lesson Breakdown
- Analyze real-world grass photo
- Adjust Vray Fur settings
- Create Grass material
More Control
You can use custom maps to control the direction and variation of the following parameters: bend direction, Initial direction, length, thickness, gravity, bend, and density.
In the example below I’ve used a single RGB map (watercolors painting that I’ve downloaded from the web) to control the bend direction of the grass. you can add any map or create your own to get a specific look.

The color map which affected the bend direction:

in the diagram below you can see the direction flow of the fur, represented by arrows, on top of the RGB color wheel:
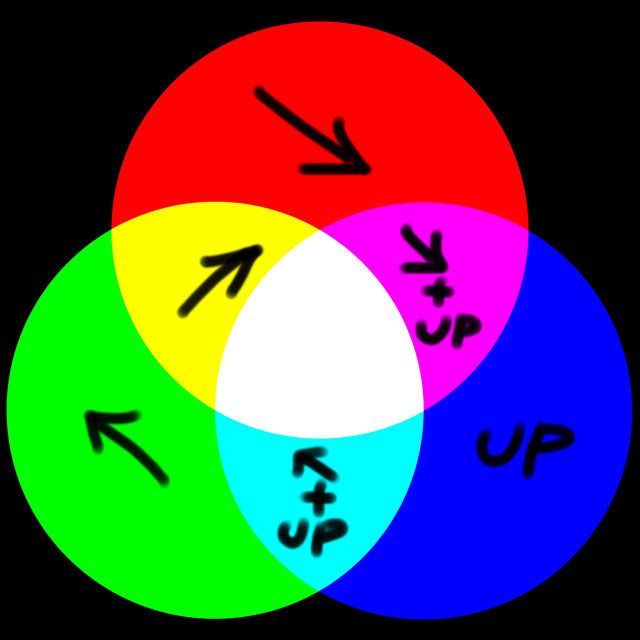






Hello,
This is a great tutorial, thank you! Can you tell me how you apply the water color map? I don’t see the link anywhere. Thank you!
hi, you can add the map under the “maps” section of the modifier.
I opened your data set in 3dsMax 2017 with vray 3, and the result is awful, could someone post a converted version or please tell me what settings need changed to make this look like the examples above.
Thanks.
Very nice! Thanks for the tutorial.
sir,if i want the fur to dynamic… how to control?
i was put the noise map in to vrayfur bend map,but render out is not look like wind Influence…how do i do ?
Both concepts nicely explained. Thank for the tutorial and hope to see more of your tutorials.
hello
Good Day
can share soft copy of ur 3ds max file
check out the download link above the video